(as of May 15, 2020)
The Imperial College London model forecasts the number of deaths in the upcoming week by country and analyzes case ascertainment per country.
The NPIM projected 2.2 million US deaths might occur in an “unmitigated” scenario, whereby transmission suppression policies were not instituted to slow or prevent spread of the virus. This initial estimate, published on March 17th, was among the first distributed to the White House, prompting the US government to take drastic actions, such as extensive travel restrictions, to mitigate the spread of the virus.
It is a transmission-based SIR model. Like other SIR models, this model examines individuals/groups of individuals — e.g. school children, household sizes, and workplace distributions — according to population density data and census data, as well as their set of contacts, to simulate transmission rates in a community. This model examines the number of projected US cases and deaths. The model makes forecasts over the next year until April 2021.
The model’s main objective: Forecast the number of deaths in the week ahead for countries with active transmission.
- Active transmission is defined as having at least 100 deaths reported overall and at least 10 deaths observed in the past 2 weeks.
- Deaths, instead of cases, are forecasted because the reporting of deaths is presumed to be more reliable and stable over time.
- The active estimates of transmissibility reflect the epidemiological state of COVID-19 at the time of infection for the deaths the present model is based upon. Therefore, the impact of controls on estimated transmissibility will be quantifiable with a delay between transmission and death.
The secondary objective: to analyze case ascertainment per country.
- We use the number of reported deaths and of cases reported with a delay (delay from reporting to deaths, see Case Ascertainment method) to analyze the reporting trends per country.
- If the reporting of cases and deaths were perfect, and the delay between reporting and death is known, the ratio of deaths to delayed cases would equal the Case Fatality Ratio (CFR).
The key assumptions behind the model are:
- The underlying mean Case Fatality Ratio is 1.38% (95% CI (1.23 – 1.53))
- The assumed delay from a case being reported to death is a mean of 10 days with a standard deviation of 2 days.
- It is assumed that all deaths due to COVID-19 have been reported in each country. Even if deaths are not under-reported, constant reporting rate is assumed over time.
The Imperial College London Model uses 3 different models, each of which deploys complex mathematical modeling with differing assumptions about how transmissibility changes throughout the time window of interest. These 3 models that estimate transmissibility are being averaged to create a final model for each country.
While this model integrates significant levels of population data, its limitations arise from the assumptions the model must make about the transmissibility of the virus. For example, this model is based on the transmissibility of the virus at the contraction of the virus for those who have reportedly died. Thus, there is an inherent lag in the transmissibility data due to the time it takes for death data to be reported. Furthermore, the true infectivity rate of the virus in symptomatic or asymptomatic is unknown. Even small miscalculations of the infectivity rate in the model can cause drastic changes in modeling predictions. Infection rates can still represent an estimation, based on testing capabilities in that country, of the virus’s true characteristics.
A previous version of the model (as of March 16, 2020):
A previous version of the model was somewhat different, and included assumptions that are no longer used in the current version. It examined the number of projected US cases and deaths across a range of various mitigation and suppression scenarios. It made forecasts over the next year until April 2021.
The assumptions in the prior version of the model were:
- Viral transmission
- One third of transmission is assumed to occur in the household, one third in schools and workplaces and the remaining third in the community, based on population density and census data concerning households, workplaces, schools and the community.
- Incubation period was estimated to be 5.1 days.
- Infectiousness was assumed to occur from 12 hours prior to the onset of symptoms for those that are symptomatic and to 4.6 days after infection in those that are asymptomatic
- Symptomatic individuals are assumed to be 50% more infectious than asymptomatic individuals.
- After recovery from infection, individuals are assumed to have short-term immunity to reinfection.
- Hospitalizations
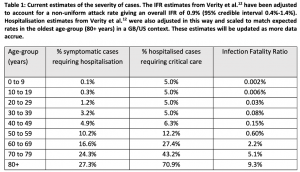
- In table 1 (from published model), the age-stratified proportion of infections that require hospitalization and the infection fatality ratio (IFR) were obtained from an analysis of a subset of cases from China
- 30% of those that are hospitalized will require critical care (defined as invasive mechanical ventilation or ECMO)
- 50% of those in critical care will die and an age-dependent proportion of those that do not require critical care die
- The bed demand numbers assume a total duration of stay in hospital of 8 days if critical care is not required and 16 days (with 10 days in ICU) if critical care is required.
- Duration of hospitalization of 10.4 days
The Imperial College London previously integrated different Non-Pharmaceutical Interventions (NPI) into their modeling to determine the best policy strategy to control COVID-19. These NPI are no longer included in the model. Rather, the model relies on current data and transmissibility estimates.
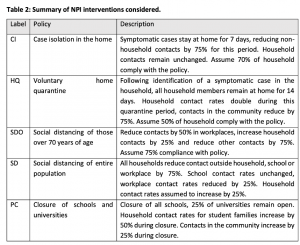
The previous version of the model included these Non-Pharmaceutical Interventions (descriptions in Table 2, from published model):
- Case isolation and voluntary home quarantine are triggered by the onset of symptoms and are implemented the next day.
- Social distancing of those over 70 years, social distancing of the entire population, stopping mass gatherings and closure of schools and universities are decisions made at the government level. In the case of lightened social distancing measures, surveillance triggers, or defined case thresholds that will indicate the need for re-implementation of social distancing, should be based on testing of patients in critical care (intensive care units, ICUs).
- Policies are assumed to be in force for 3 months, other than social distancing of those over the age of 70 which is assumed to remain in place for one month longer. Suppression strategies are assumed to be in place for 5 months or longer.
Relative to each NPI intervention, the model uses the described assumptions to provide the following output predictions:
- Total deaths
- Peak ICU beds
- Proportion of time with social distancing in place

